ভেক্টর (Vector) অনেক ধরনের হতে পারে। তবে খুব সাধারণভাবে বলতে গেলে নিচে উল্লিখিত ধরনের ভেক্টর সম্পর্কে জানা থাকা ভালো-
১। স্বাধীন ভেক্টর (Free Vector)
স্বাধীন ভেক্টর বলতে এমন একটি ভেক্টর রাশিকে বোঝায়, যার পাদবিন্দু বা স্থানাঙ্ক (origin) যেকোনো স্থানে নির্ধারণ করা যায়। অর্থাৎ, এই ভেক্টরটির গুণাগুণ পরিবর্তন না করে আমরা এটি স্থানান্তরিত করতে পারি। স্বাধীন ভেক্টরের মূল বৈশিষ্ট্য হলো এর পরিমাণ এবং দিক, কিন্তু এর পাদবিন্দু পরিবর্তন করা সম্ভব।
উদাহরণ:
ধরা যাক, আমাদের কাছে 5 N (নিউটন) মানের একটি বল আছে, যা পূর্বমুখী। এখানে:
-
পরিমাণ: 5 N
-
দিক: পূর্ব
এখন, এই বলটি যেকোনো স্থানে স্থানান্তর করা যেতে পারে, এবং এটি স্থানান্তরের ফলে ভেক্টরের গুণগত বৈশিষ্ট্যগুলো অপরিবর্তিত থাকবে। যেমন, আমরা যদি বলটি A পয়েন্ট থেকে B পয়েন্টে সরিয়ে দেই, তবে এটি এখনও 5 N মানের পূর্বমুখী বল হিসেবেই থাকবে।
স্বাধীন ভেক্টরের ব্যবহার:
স্বাধীন ভেক্টরের ব্যবহার বেশ কিছু ক্ষেত্রে দেখা যায়, যেমন:
-
পদার্থবিজ্ঞান: যেখানে বলের পরিমাণ এবং দিক বোঝাতে হয়।
-
যান্ত্রিক ইঞ্জিনিয়ারিং: যেখানে শক্তি এবং চাপের বিভিন্ন অবস্থান বিশ্লেষণ করা হয়।
সারসংক্ষেপ:
স্বাধীন ভেক্টরগুলোর স্থানাঙ্ক পরিবর্তন করা সম্ভব, তবে এদের গুণ এবং দিক অপরিবর্তিত থাকে। এটি পদার্থবিজ্ঞান ও প্রকৌশল ক্ষেত্রে ভেক্টরের বিশ্লেষণে একটি গুরুত্বপূর্ণ ধারণা।
২। সীমাবদ্ধ ভেক্টর (Localized Vector)
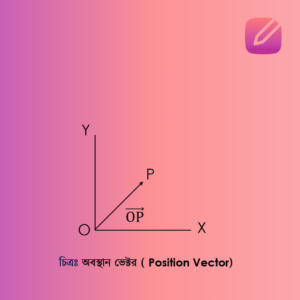
সীমাবদ্ধ ভেক্টর বলতে এমন একটি ভেক্টর রাশিকে বোঝায়, যার পাদবিন্দু বা স্থানাঙ্ক নির্দিষ্টভাবে স্থির করা হয়। অর্থাৎ, এই ভেক্টরের পাদবিন্দু পরিবর্তন করা সম্ভব নয় এবং এটি একটি নির্দিষ্ট বিন্দু থেকে আঁকা হয়। সীমাবদ্ধ ভেক্টরের দিক ও পরিমাণ ঠিক থাকলেও, এটি যেকোনো স্থানান্তরের মাধ্যমে পুনরায় নির্মাণ করা যায় না।
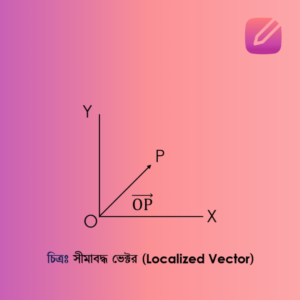
উদাহরণ:
ধরা যাক, আমাদের কাছে একটি অবস্থান ভেক্টর আছে, যা আমাদের কোনো বস্তুর অবস্থান নির্দেশ করে। এখানে:
-
পাদবিন্দু: এটি একটি নির্দিষ্ট বিন্দু (যেমন, একটি তল বা মানচিত্রের মূলবিন্দু) থেকে নির্ধারিত হয়।
-
দিক: এটি সেই নির্দিষ্ট বিন্দু থেকে নির্ধারিত হয়ে থাকে।
যেহেতু এই ভেক্টরটি একটি নির্দিষ্ট বিন্দু থেকে আঁকা হয়, তাই এটি একটি সীমাবদ্ধ ভেক্টর হিসেবে গণ্য হয়। উদাহরণস্বরূপ, যদি আমরা বলি যে একটি গাড়ি A পয়েন্টে অবস্থান করছে এবং এটি B পয়েন্টে যাচ্ছে, তবে গাড়ির অবস্থান ভেক্টর হবে সীমাবদ্ধ, কারণ এটি A পয়েন্ট থেকে শুরু হয়।
সীমাবদ্ধ ভেক্টরের ব্যবহার:
সীমাবদ্ধ ভেক্টরের ব্যবহার বিশেষত নিম্নলিখিত ক্ষেত্রে লক্ষ্য করা যায়:
-
পদার্থবিজ্ঞান: যেখানে বস্তুর অবস্থান এবং গতিবিধি বিশ্লেষণ করতে হয়।
-
যান্ত্রিক ইঞ্জিনিয়ারিং: যেখানে কাঠামোগত বিশ্লেষণ ও নকশায় নির্দিষ্ট বিন্দু থেকে শক্তির প্রয়োগ বোঝাতে হয়।
সারসংক্ষেপ:
সীমাবদ্ধ ভেক্টরগুলোর পাদবিন্দু একটি নির্দিষ্ট স্থানে স্থির থাকে, এবং এটি সেই স্থান থেকে নির্দেশিত হয়। এই ভেক্টরের গুণগত বৈশিষ্ট্য এবং দিক অপরিবর্তিত থাকলেও, এর পাদবিন্দু পরিবর্তন করা সম্ভব নয়, যা পদার্থবিজ্ঞানে ও প্রকৌশলে ভেক্টরের বিশ্লেষণের জন্য অত্যন্ত গুরুত্বপূর্ণ।
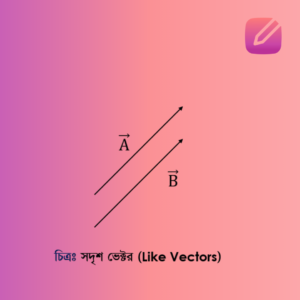
৩। সদৃশ ভেক্টর (Like Vectors)
সমজাতীয় দুই বা ততোধিক ভেক্টর যদি একই দিকে ক্রিয়া করে, তবে তাদেরকে সদৃশ বা সমান্তরাল ভেক্টর বলে। এই ধরনের ভেক্টরগুলোর দিক এবং প্রকৃতি একই থাকে, যদিও তাদের পরিমাণ আলাদা হতে পারে।
উদাহরণ:
ধরা যাক, চিত্রে A→A এবং B→B দুটি ভেক্টর আছে। এখানে:
- A→A ভেক্টর: এটি একটি নির্দিষ্ট পরিমাণ এবং দিক নির্দেশ করে।
- B→B ভেক্টর: এটি একটি ভিন্ন পরিমাণ নির্দেশ করতে পারে, কিন্তু এর দিক A→A ভেক্টরের দিকের সাথে মিলে যায়।
যেহেতু A→A এবং B→B একই দিকে ক্রিয়া করে, তাই এগুলোকে সদৃশ ভেক্টর বলা হয়।
সদৃশ ভেক্টরের বৈশিষ্ট্য:
- দিক: দুটি ভেক্টরের দিক একই হতে হবে।
- প্রকৃতি: ভেক্টরগুলো সমজাতীয় হতে হবে (যেমন, উভয়ই বলের ভেক্টর বা উভয়ই স্থানান্তরের ভেক্টর)।
- পরিমাণ: ভেক্টরগুলোর পরিমাণ আলাদা হতে পারে, তবে তা সদৃশ ভেক্টর হওয়ার জন্য বাধা সৃষ্টি করে না।
সদৃশ ভেক্টরের ব্যবহার:
সদৃশ ভেক্টরের ব্যবহার বিভিন্ন ক্ষেত্রে দেখা যায়, যেমন:
- পদার্থবিজ্ঞান: যেখানে বিভিন্ন বল একই দিক থেকে ক্রিয়া করে।
- ইঞ্জিনিয়ারিং: যেখানে কাঠামোর উপর বিভিন্ন স্থান থেকে একই দিকের চাপ বা শক্তি প্রয়োগ করা হয়।
সারসংক্ষেপ:
সদৃশ ভেক্টরগুলোর দিক এবং প্রকৃতি একই থাকে, যদিও তাদের পরিমাণ ভিন্ন হতে পারে। এই ভেক্টরগুলো বিভিন্ন বৈজ্ঞানিক ও প্রকৌশল ক্ষেত্রে গুরুত্বপূর্ণ ভূমিকা পালন করে, কারণ এদের মাধ্যমে বিভিন্ন বল ও শক্তির সম্মিলিত প্রভাব বিশ্লেষণ করা যায়।
৪। বিসদৃশ ভেক্টর (Unlike Vectors)
সমজাতীয় দুটি ভেক্টর যদি বিপরীত দিকে ক্রিয়া করে, তবে তাদেরকে বিসদৃশ ভেক্টর বলা হয়। এই ধরনের ভেক্টরগুলোর পরিমাণ আলাদা হতে পারে, তবে তাদের দিক বিপরীত হয়।
উদাহরণ:
ধরা যাক, চিত্রে A→A এবং B→B দুটি ভেক্টর আছে। এখানে:
- A→A ভেক্টর: এটি একটি নির্দিষ্ট পরিমাণ এবং একটি নির্দিষ্ট দিকে নির্দেশ করে।
- B→B ভেক্টর: এটি একটি ভিন্ন পরিমাণ নির্দেশ করতে পারে, কিন্তু এর দিক A→A ভেক্টরের বিপরীত।
যেহেতু A→A এবং B→B ভেক্টর বিপরীত দিকে ক্রিয়া করে, তাই এগুলোকে বিসদৃশ ভেক্টর বলা হয়।
বিসদৃশ ভেক্টরের বৈশিষ্ট্য:
- দিক: দুটি ভেক্টরের দিক বিপরীত হতে হবে।
- প্রকৃতি: ভেক্টরগুলো সমজাতীয় হতে হবে (যেমন, উভয়ই বলের ভেক্টর বা উভয়ই স্থানান্তরের ভেক্টর)।
- পরিমাণ: ভেক্টরগুলোর পরিমাণ আলাদা হতে পারে, তবে তা বিসদৃশ ভেক্টর হওয়ার জন্য বাধা সৃষ্টি করে না।
বিসদৃশ ভেক্টরের ব্যবহার:
বিসদৃশ ভেক্টরের ব্যবহার বিভিন্ন ক্ষেত্রে দেখা যায়, যেমন:
- পদার্থবিজ্ঞান: যেখানে বিভিন্ন বল বিপরীত দিক থেকে ক্রিয়া করে, যেমন কোনও বস্তুতে একদিকে টান আর অন্যদিকে চাপ।
- ইঞ্জিনিয়ারিং: যেখানে কাঠামোর উপর বিভিন্ন স্থান থেকে বিপরীত দিকের চাপ বা শক্তি প্রয়োগ করা হয়।
সারসংক্ষেপ:
বিসদৃশ ভেক্টরগুলোর দিক বিপরীত থাকে, যদিও তাদের পরিমাণ ভিন্ন হতে পারে। এই ভেক্টরগুলো বিভিন্ন বৈজ্ঞানিক ও প্রকৌশল ক্ষেত্রে গুরুত্বপূর্ণ ভূমিকা পালন করে, কারণ এদের মাধ্যমে বিভিন্ন বিপরীত বল ও শক্তির সম্মিলিত প্রভাব বিশ্লেষণ করা যায়।
৫। সমান ভেক্টর (Equal Vectors)
সমজাতীয় দুটি ভেক্টরের পরিমাণ যদি সমান হয় এবং তাদের দিক যদি একই দিকে হয়, তবে তাদেরকে সমান ভেক্টর বলা হয়। অর্থাৎ, দুটি ভেক্টরের পরিমাণ এবং দিক উভয়ই একে অপরের সমান হলে সেই ভেক্টরগুলো সমান ভেক্টর হিসেবে গণ্য হবে।
উদাহরণ:
ধরা যাক, চিত্রে A→A এবং B→B দুটি ভেক্টর আছে। এখানে:
- A→A ভেক্টর: এটি একটি নির্দিষ্ট পরিমাণ এবং একটি নির্দিষ্ট দিকে নির্দেশ করে।
- B→B ভেক্টর: এর পরিমাণ এবং দিক A→A ভেক্টরের পরিমাণ ও দিকের সাথে মিলিত।
যেহেতু A→A এবং B→B ভেক্টরের পরিমাণ এবং দিক একই, তাই এগুলোকে সমান ভেক্টর বলা হয়। অর্থাৎ, A→A = B→B।
সমান ভেক্টরের বৈশিষ্ট্য:
- পরিমাণ: দুটি ভেক্টরের পরিমাণ একে অপরের সমান হতে হবে।
- দিক: দুটি ভেক্টরের দিকও একই হতে হবে।
- প্রকৃতি: ভেক্টরগুলো সমজাতীয় হতে হবে (যেমন, উভয়ই বলের ভেক্টর বা উভয়ই স্থানান্তরের ভেক্টর)।
সমান ভেক্টরের ব্যবহার:
সমান ভেক্টরের ব্যবহার বিভিন্ন ক্ষেত্রে দেখা যায়, যেমন:
- পদার্থবিজ্ঞান: যেখানে বিভিন্ন বল একই পরিমাণ এবং দিক থেকে ক্রিয়া করে।
- ইঞ্জিনিয়ারিং: যেখানে কাঠামোর উপর বিভিন্ন স্থানে একই পরিমাণ এবং দিকের চাপ বা শক্তি প্রয়োগ করা হয়।
সারসংক্ষেপ:
সমান ভেক্টরগুলোর পরিমাণ এবং দিক উভয়ই একে অপরের সমান হয়। এই ভেক্টরগুলো বিভিন্ন বৈজ্ঞানিক ও প্রকৌশল ক্ষেত্রে গুরুত্বপূর্ণ ভূমিকা পালন করে, কারণ এদের মাধ্যমে বিভিন্ন সমান পরিমাণ এবং দিকের বল ও শক্তির সম্মিলিত প্রভাব বিশ্লেষণ করা যায়।
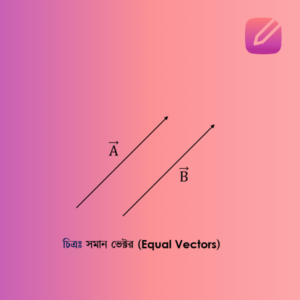
দুটি ভেক্টরের সমতা ভেক্টরদ্বয়ের পাদবিন্দুর অবস্থানের উপর নির্ভর করে না। পাদবিন্দু যেখানেই থাকুক না কেন যদি ভেক্টরদ্বয়ের মান সমান এবং দিক একই দিকে হয়, তাহলেই তারা সমান ভেক্টর হবে। একই দিকে নির্দেশিত সমান। দৈর্ঘ্যের দুটি সমান্তরাল রেখা দিয়ে দুটি সমান ভেক্টর বোঝানো হয়।
৬। ঋণাত্মক বা বিপরীত ভেক্টর (Negative Vector)
নির্দিষ্ট দিক বরাবর কোনো ভেক্টরকে ধনাত্মক ধরলে, তার বিপরীত দিকে সমমানের সমজাতীয় ভেক্টরকে ঋণাত্মক ভেক্টর বা বিপরীত ভেক্টর বলা হয়। অর্থাৎ, যদি একটি ভেক্টরের দিক ধনাত্মক হয়, তবে তার বিপরীত দিকের ভেক্টরটি ঋণাত্মক হবে এবং উভয়ের পরিমাণ সমান থাকবে।
উদাহরণ:
ধরা যাক, চিত্রে PQ→=A এবং QP→=−A দুটি ভেক্টর আছে। এখানে:
- PQ→ = A: এটি একটি নির্দিষ্ট পরিমাণ এবং একটি নির্দিষ্ট দিক নির্দেশ করে।
- QP→ = −A: এটি PQ→ এর বিপরীত দিকে নির্দেশ করে এবং এর পরিমাণ PQ→ এর সমান কিন্তু দিক বিপরীত।
যেহেতু PQ→ এবং QP→ ভেক্টরের পরিমাণ সমান কিন্তু দিক বিপরীত, তাই QP→ কে PQ→ এর ঋণাত্মক বা বিপরীত ভেক্টর বলা হয়।
ঋণাত্মক ভেক্টরের বৈশিষ্ট্য:
- পরিমাণ: দুটি ভেক্টরের পরিমাণ সমান হতে হবে।
- দিক: দুটি ভেক্টরের দিক বিপরীত হতে হবে।
- প্রকৃতি: ভেক্টরগুলো সমজাতীয় হতে হবে (যেমন, উভয়ই বলের ভেক্টর বা উভয়ই স্থানান্তরের ভেক্টর)।
ঋণাত্মক ভেক্টরের ব্যবহার:
ঋণাত্মক ভেক্টরের ব্যবহার বিভিন্ন ক্ষেত্রে দেখা যায়, যেমন:
- পদার্থবিজ্ঞান: যেখানে কোনো বস্তুর উপর বিপরীতমুখী বলের প্রভাব বিশ্লেষণ করতে হয়।
- ইঞ্জিনিয়ারিং: যেখানে কাঠামোর উপর বিপরীত দিক থেকে চাপ বা শক্তি প্রয়োগ করা হয়।
সারসংক্ষেপ:
ঋণাত্মক বা বিপরীত ভেক্টর হলো এমন ভেক্টর, যার পরিমাণ ধনাত্মক ভেক্টরের সমান কিন্তু দিক বিপরীত। এই ভেক্টরগুলো বিভিন্ন বৈজ্ঞানিক ও প্রকৌশল ক্ষেত্রে গুরুত্বপূর্ণ ভূমিকা পালন করে, কারণ এদের মাধ্যমে বিপরীতমুখী বল ও শক্তির সম্মিলিত প্রভাব বিশ্লেষণ করা যায়।
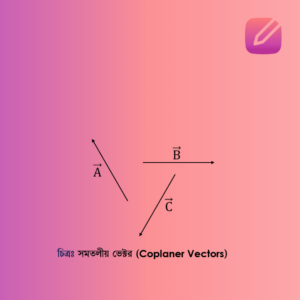
৭। সমরেখ ভেক্টর (Collinear Vectors)
দুই বা ততোধিক ভেক্টর যদি একই সরলরেখা বরাবর বা পরস্পর সমান্তরালে ক্রিয়া করে, তবে তাদেরকে সমরেখ ভেক্টর বলা হয়। অর্থাৎ, এই ভেক্টরগুলো একই রেখার উপর অবস্থিত থাকে বা একে অপরের সমান্তরালে অবস্থান করে।
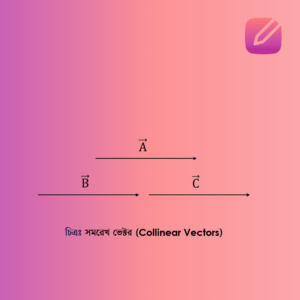
উদাহরণ:
ধরা যাক, চিত্রে A⃗, B⃗, এবং C⃗ ভেক্টরগুলো রয়েছে। এখানে:
- A⃗: এটি একটি নির্দিষ্ট পরিমাণ এবং দিক নির্দেশ করে।
- B⃗: এটি একই রেখার উপর বা A⃗ এর সমান্তরালে অবস্থিত এবং এর পরিমাণ ও দিক A⃗ এর সাথে সামঞ্জস্যপূর্ণ হতে পারে।
- C⃗: এটি একই রেখার উপর বা A⃗ ও B⃗ এর সমান্তরালে অবস্থিত।
যেহেতু A⃗, B⃗, এবং C⃗ একই সরলরেখা বরাবর বা পরস্পর সমান্তরালে ক্রিয়া করে, তাই এদেরকে সমরেখ ভেক্টর বলা হয়।
সমরেখ ভেক্টরের বৈশিষ্ট্য:
- সরলরেখা বরাবর: ভেক্টরগুলো একই সরলরেখার বরাবর অবস্থান করবে।
- সমান্তরাল: ভেক্টরগুলো একে অপরের সমান্তরালে থাকতে পারে।
- প্রকৃতি: ভেক্টরগুলো সমজাতীয় হতে হবে (যেমন, উভয়ই বলের ভেক্টর বা উভয়ই স্থানান্তরের ভেক্টর)।
সমরেখ ভেক্টরের ব্যবহার:
সমরেখ ভেক্টরের ব্যবহার বিভিন্ন ক্ষেত্রে দেখা যায়, যেমন:
- পদার্থবিজ্ঞান: যেখানে বিভিন্ন বল একই রেখার বরাবর ক্রিয়া করে।
- ইঞ্জিনিয়ারিং: যেখানে কাঠামোর উপর বিভিন্ন স্থানে একই রেখার বরাবর চাপ বা শক্তি প্রয়োগ করা হয়।
সারসংক্ষেপ:
সমরেখ ভেক্টর হলো এমন ভেক্টর, যা একই সরলরেখা বরাবর বা পরস্পর সমান্তরালে ক্রিয়া করে। এই ভেক্টরগুলো বিভিন্ন বৈজ্ঞানিক ও প্রকৌশল ক্ষেত্রে গুরুত্বপূর্ণ ভূমিকা পালন করে, কারণ এদের মাধ্যমে বিভিন্ন রেখাবর্তী বল ও শক্তির সম্মিলিত প্রভাব বিশ্লেষণ করা যায়।
৮। সমতলীয় ভেক্টর (Coplanar Vectors)
দুই বা ততোধিক ভেক্টর যদি একই সমতলে অবস্থিত হয়, তবে তাদেরকে সমতলীয় ভেক্টর বলা হয়। অর্থাৎ, এই ভেক্টরগুলো একটি সমতলের মধ্যে অবস্থান করে এবং তাদের ক্রিয়ার ক্ষেত্র একই সমতলে থাকে।
উদাহরণ:
ধরা যাক, চিত্রে A⃗, B⃗, এবং C⃗ ভেক্টরগুলো রয়েছে। এখানে:
- A⃗: এটি একটি নির্দিষ্ট পরিমাণ এবং দিক নির্দেশ করে, যা একটি নির্দিষ্ট সমতলের মধ্যে অবস্থিত।
- B⃗: এটি একই সমতলের মধ্যে অবস্থিত এবং এর পরিমাণ ও দিক A⃗ এর সাথে সামঞ্জস্যপূর্ণ হতে পারে।
- C⃗: এটি একই সমতলের মধ্যে অবস্থিত।
যেহেতু A⃗, B⃗, এবং C⃗ একই সমতলের মধ্যে অবস্থান করে, তাই এদেরকে সমতলীয় ভেক্টর বলা হয়।
সমতলীয় ভেক্টরের বৈশিষ্ট্য:
- একই সমতলে অবস্থান: ভেক্টরগুলো একই সমতলের মধ্যে অবস্থান করবে।
- প্রকৃতি: ভেক্টরগুলো সমজাতীয় হতে হবে (যেমন, উভয়ই বলের ভেক্টর বা উভয়ই স্থানান্তরের ভেক্টর)।
- দিক ও পরিমাণ: ভেক্টরগুলোর দিক ও পরিমাণ যেকোনো হতে পারে, তবে তারা একই সমতলে থাকতে হবে।
সমতলীয় ভেক্টরের ব্যবহার:
সমতলীয় ভেক্টরের ব্যবহার বিভিন্ন ক্ষেত্রে দেখা যায়, যেমন:
- পদার্থবিজ্ঞান: যেখানে বিভিন্ন বল একই সমতলে ক্রিয়া করে।
- ইঞ্জিনিয়ারিং: যেখানে কাঠামোর উপর বিভিন্ন স্থানে একই সমতলে চাপ বা শক্তি প্রয়োগ করা হয়।
সারসংক্ষেপ:
সমতলীয় ভেক্টর হলো এমন ভেক্টর, যা একই সমতলে অবস্থিত। এই ভেক্টরগুলো বিভিন্ন বৈজ্ঞানিক ও প্রকৌশল ক্ষেত্রে গুরুত্বপূর্ণ ভূমিকা পালন করে, কারণ এদের মাধ্যমে বিভিন্ন সমতলীয় বল ও শক্তির সম্মিলিত প্রভাব বিশ্লেষণ করা যায়।
৯। সঠিক ভেক্টর (Proper Vectors)
যে সকল ভেক্টরের মান শূন্য নয়, তাদেরকে সঠিক ভেক্টর বলে। অর্থাৎ, যেসব ভেক্টরের একটি নির্দিষ্ট পরিমাণ এবং দিক থাকে এবং এই পরিমাণটি শূন্যের থেকে বেশি, সেই ভেক্টরগুলো সঠিক ভেক্টর হিসেবে গণ্য হয়।
উদাহরণ:
- A⃗: যদি A⃗ ভেক্টরের পরিমাণ শূন্য না হয়, তবে এটি একটি সঠিক ভেক্টর।
- B⃗: যদি B⃗ ভেক্টরের পরিমাণ শূন্য না হয়, তবে এটিও একটি সঠিক ভেক্টর।
সঠিক ভেক্টরের বৈশিষ্ট্য:
- পরিমাণ: ভেক্টরের পরিমাণ শূন্যের থেকে বেশি হবে।
- দিক: ভেক্টরের একটি নির্দিষ্ট দিক থাকবে।
- প্রকৃতি: ভেক্টরগুলো সমজাতীয় হতে হবে (যেমন, উভয়ই বলের ভেক্টর বা উভয়ই স্থানান্তরের ভেক্টর)।
সঠিক ভেক্টরের ব্যবহার:
সঠিক ভেক্টরের ব্যবহার বিভিন্ন ক্ষেত্রে দেখা যায়, যেমন:
- পদার্থবিজ্ঞান: যেখানে বিভিন্ন বলের মান শূন্যের থেকে বেশি এবং নির্দিষ্ট দিক থেকে ক্রিয়া করে।
- ইঞ্জিনিয়ারিং: যেখানে কাঠামোর উপর বিভিন্ন স্থানে নির্দিষ্ট পরিমাণের চাপ বা শক্তি প্রয়োগ করা হয়।
সারসংক্ষেপ:
সঠিক ভেক্টর হলো এমন ভেক্টর, যার মান শূন্য নয় এবং যার একটি নির্দিষ্ট দিক রয়েছে। এই ভেক্টরগুলো বিভিন্ন বৈজ্ঞানিক ও প্রকৌশল ক্ষেত্রে গুরুত্বপূর্ণ ভূমিকা পালন করে, কারণ এদের মাধ্যমে বিভিন্ন বল ও শক্তির সম্মিলিত প্রভাব বিশ্লেষণ করা যায়।
১০। নাল ভেক্টর বা শূন্য ভেক্টর (Null Vector)
যে ভেক্টরের মান শূন্য, তাকে নাল ভেক্টর বা শূন্য ভেক্টর বলা হয়। একটি ভেক্টরের সাথে তার বিপরীত ভেক্টর যোগ করে বা দুটি সমান ভেক্টর বিয়োগ করে নাল ভেক্টর পাওয়া যায়। নাল ভেক্টরের পাদবিন্দু এবং শীর্ষবিন্দু একই বিন্দুতে অবস্থান করে।
বৈশিষ্ট্য:
- মান: নাল ভেক্টরের মান শূন্য।
- দিক: নাল ভেক্টরের কোনো সুনির্দিষ্ট দিক নেই।
- পদবিন্দু ও শীর্ষবিন্দু: নাল ভেক্টরের পদবিন্দু এবং শীর্ষবিন্দু একই বিন্দুতে অবস্থান করে।
উদাহরণ:
- 0→: এটি নাল ভেক্টরের প্রতীক, যা নির্দেশ করে যে ভেক্টরের মান শূন্য।
নাল ভেক্টরের প্রাপ্তি:
- যোগফল: একটি ভেক্টরের সাথে তার বিপরীত ভেক্টর যোগ করলে নাল ভেক্টর পাওয়া যায়।
- উদাহরণ: A⃗ + (-A⃗) = 0→
- বিয়োগফল: দুটি সমান ভেক্টর বিয়োগ করলে নাল ভেক্টর পাওয়া যায়।
- উদাহরণ: A⃗ – A⃗ = 0→
নাল ভেক্টরের ব্যবহার:
নাল ভেক্টরের ব্যবহার বিভিন্ন ক্ষেত্রে দেখা যায়, যেমন:
- পদার্থবিজ্ঞান: যেখানে বিভিন্ন বলের যোগফল শূন্য হয়।
- গণিত: বিভিন্ন ভেক্টর গণনায়, যেখানে ভেক্টরগুলোর পার্থক্য শূন্য হয়।
সারসংক্ষেপ:
নাল ভেক্টর হলো এমন একটি ভেক্টর যার মান শূন্য এবং যার কোনো নির্দিষ্ট দিক নেই। এটি বিভিন্ন বৈজ্ঞানিক ও প্রকৌশল ক্ষেত্রে গুরুত্বপূর্ণ ভূমিকা পালন করে, কারণ এদের মাধ্যমে বিভিন্ন বল ও শক্তির সম্মিলিত প্রভাব বিশ্লেষণ করা যায়।
১১। একক ভেক্টর (Unit Vector)
কোনো ভেক্টরের মান যদি একক হয়, তাহলে তাকে একক ভেক্টর বলে। কোনো ভেক্টরের মান যদি শূন্য না হয়, তাহলে সেই ভেক্টরকে তার মান দিয়ে ভাগ করলে সেই ভেক্টরের দিকে নির্দেশিত একটি একক ভেক্টর পাওয়া যায়।
উদাহরণ:
ধরা যাক, A⃗\vec{A} একটি ভেক্টর যার সংখ্যাগত মান A≠0A \neq 0। তাহলে A⃗\vec{A} ভেক্টরকে AA দ্বারা ভাগ করলে a⃗\vec{a} নামে একটি একক ভেক্টর পাওয়া যায়। অর্থাৎ,
a⃗=A⃗A\vec{a} = \frac{\vec{A}}{A}
এখানে a⃗\vec{a} হলো একক ভেক্টর, যার মান একক এবং দিক A⃗\vec{A} এর দিকে নির্দেশিত।
একক ভেক্টরের গুরুত্ব:
ভেক্টরের আলোচনায় একক ভেক্টরের গুরুত্ব অপরিসীম। অনেক সময় একক ভেক্টরের আলাদা সংকেত ব্যবহার করা হয় এবং তা হচ্ছে অক্ষরের উপরে তীর চিহ্নের পরিবর্তে টুপি (cap) বা হ্যাট (hat) চিহ্ন (^\hat{})। যেমন a^\hat{a} বা i^\hat{i}।
উদাহরণ চিত্র:
ধরা যাক, A⃗=5a^\vec{A} = 5 \hat{a}। এখানে, a^\hat{a} একটি একক ভেক্টর এবং A⃗\vec{A} এর মান 5।
সংক্ষেপে:
- একক ভেক্টর: যার মান একক এবং দিক নির্দিষ্ট ভেক্টরের দিকে।
- গণিত: a⃗=A⃗A\vec{a} = \frac{\vec{A}}{A}
- সংকেত: a^\hat{a} বা i^\hat{i}
একক ভেক্টর ভেক্টরের দিক নির্দেশনা ও মানের সরলীকরণের জন্য ব্যবহৃত হয় এবং ভেক্টর বিশ্লেষণে অত্যন্ত গুরুত্বপূর্ণ ভূমিকা পালন করে।
১২। অবস্থান ভেক্টর (Position Vector)
প্রসঙ্গ কাঠামোর মূল বিন্দুর সাপেক্ষে কোনো বিন্দুর অবস্থান যে ভেক্টর দিয়ে নির্দেশ করা হয়, তাকে ঐ বিন্দুর অবস্থান ভেক্টর বলে।
উদাহরণ:
চিত্রে, OO হচ্ছে প্রসঙ্গ কাঠামোর মূল বিন্দু এবং PP যে কোনো একটি বিন্দু। OP⃗\vec{OP} ভেক্টরটি OO বিন্দুর সাপেক্ষে PP বিন্দুর অবস্থান নির্দেশ করছে। এখানে OP⃗\vec{OP} একটি অবস্থান ভেক্টর।
অবস্থান ভেক্টরের সংজ্ঞা:
অবস্থান ভেক্টরকে অনেক সময় ব্যাসার্ধ ভেক্টর (radius vector) বলা হয় এবং r⃗\vec{r} দ্বারা প্রকাশ করা হয়। সুতরাং,
OP⃗=r⃗\vec{OP} = \vec{r}
বৈশিষ্ট্য:
- মূল বিন্দু: অবস্থান ভেক্টর সব সময় প্রসঙ্গ কাঠামোর মূল বিন্দু থেকে শুরু হয়।
- অবস্থান নির্দেশনা: এটি কোনো বিন্দুর অবস্থান নির্দেশ করে।
- প্রতীক: অবস্থান ভেক্টরকে সাধারণত r⃗\vec{r} দিয়ে প্রকাশ করা হয়।
উদাহরণ চিত্র:
- OO: প্রসঙ্গ কাঠামোর মূল বিন্দু
- PP: কোনো একটি বিন্দু
- OP⃗\vec{OP}: OO থেকে PP পর্যন্ত অবস্থান ভেক্টর, যা r⃗\vec{r} দিয়ে প্রকাশ করা হয়।
সারসংক্ষেপ:
অবস্থান ভেক্টর হলো একটি ভেক্টর যা প্রসঙ্গ কাঠামোর মূল বিন্দুর সাপেক্ষে কোনো বিন্দুর অবস্থান নির্দেশ করে। এটি ভেক্টরের অন্যতম প্রধান প্রকার এবং বিভিন্ন বৈজ্ঞানিক ও গণিতিক বিশ্লেষণে গুরুত্বপূর্ণ ভূমিকা পালন করে।
১৩। সরণ ভেক্টর (Displacement Vector)
কোনো বস্তুর অবস্থান ভেক্টরের পরিবর্তনকে সরণ ভেক্টর বলা হয়। সরণ ভেক্টর বস্তুর আদি অবস্থান এবং শেষ অবস্থানের মধ্যে পার্থক্য নির্দেশ করে।
সংজ্ঞা:
ধরা যাক, কোনো বস্তুর শেষ অবস্থান ভেক্টর rf⃗\vec{r_f} এবং আদি অবস্থান ভেক্টর ri⃗\vec{r_i}। এই দুই ভেক্টরের পার্থক্য হল সরণ ভেক্টর Δr⃗\Delta \vec{r}।
গাণিতিক প্রকাশ:
Δr⃗=rf⃗−ri⃗\Delta \vec{r} = \vec{r_f} – \vec{r_i}
অথবা,
Δr=rf−ri\Delta r = r_f – r_i
বৈশিষ্ট্য:
- পরিবর্তন নির্দেশনা: সরণ ভেক্টর কোনো বস্তুর স্থানান্তরের দিক এবং পরিমাণ নির্দেশ করে।
- দূরত্ব: এটি শুধুমাত্র বস্তুর আদি এবং শেষ অবস্থানের মধ্যে সরল পথের দূরত্ব নির্দেশ করে, যেটি সম্পূর্ণ যাত্রার দূরত্ব নয়।
- নেতিবাচক বা ধনাত্মক: সরণ ভেক্টরের মান নেতিবাচক বা ধনাত্মক হতে পারে, যা বস্তুর গতির দিকের উপর নির্ভর করে।
উদাহরণ:
- যদি একটি বস্তুর আদি অবস্থান AA (অবস্থান ভেক্টর ri⃗\vec{r_i}) এবং শেষ অবস্থান BB (অবস্থান ভেক্টর rf⃗\vec{r_f}) হয়, তবে সরণ ভেক্টর Δr⃗\Delta \vec{r} হলো BB থেকে AA পর্যন্ত সরল রেখা যা বস্তুর অবস্থানের পরিবর্তন নির্দেশ করে।
সারসংক্ষেপ:
সরণ ভেক্টর হলো একটি ভেক্টর যা একটি বস্তুর আদি ও শেষ অবস্থানের মধ্যে পরিবর্তন নির্দেশ করে। এটি বস্তুর স্থানান্তরের দিক এবং পরিমাণ বুঝতে সাহায্য করে এবং বিভিন্ন বিজ্ঞান ও প্রকৌশল বিশ্লেষণে গুরুত্বপূর্ণ ভূমিকা পালন করে।
১৪। বিপ্রতীপ বা ব্যতিহার ভেক্টর (Reciprocal Vector)
সমজাতীয় দুটি সমান্তরাল ভেক্টরের একটি মান যদি অপরটির বিপরীত সংখ্যা হয়, তবে তাদেরকে বিপ্রতীপ বা ব্যতিহার ভেক্টর বলা হয়। অর্থাৎ, যদি দুটি ভেক্টরের একটির মান এবং দিক অপরটির মান এবং দিকের বিপরীত হয়, তবে সেগুলোকে বিপ্রতীপ ভেক্টর হিসেবে গণ্য করা হয়।
উদাহরণ:
ধরা যাক:
- A⃗=7i^\vec{A} = 7 \hat{i}
- B⃗=−7i^\vec{B} = -7 \hat{i}
এখানে, A⃗\vec{A} এবং B⃗\vec{B} পরস্পর বিপ্রতীপ ভেক্টর। অর্থাৎ, A⃗\vec{A} এর মান 77 এবং এর দিক +i^+ \hat{i} নির্দেশ করছে, যখন B⃗\vec{B} এর মান −7-7 এবং এর দিক −i^- \hat{i} নির্দেশ করছে।
বৈশিষ্ট্য:
- দিক: বিপ্রতীপ ভেক্টরের দিক পরস্পর বিপরীত।
- মান: বিপ্রতীপ ভেক্টরের মান একে অপরের সমান, কিন্তু চিহ্ন ভিন্ন।
- প্রকার: এই ভেক্টরগুলো সাধারণত সমজাতীয় এবং সমান্তরাল হয়।
সারসংক্ষেপ:
বিপ্রতীপ বা ব্যতিহার ভেক্টর হলো এমন ভেক্টর যেগুলোর একটির মান অপরটির বিপরীত সংখ্যা এবং দিকও বিপরীত। এই ভেক্টরগুলো ভেক্টর বিশ্লেষণে গুরুত্বপূর্ণ, কারণ তারা বিভিন্ন বল ও গতির পারস্পরিক সম্পর্ক বুঝতে সাহায্য করে।